Formation Juge-Arbitre - JAT
Responsable de formation
Marc Éluard - Formateur Fédéral
Formateurs
Hervé Thévenon - Formateur Fédéral
Mehdi Lambert - Formateur Ligue
version 2.3.3.0 - septembre 2025 Copyright © Marc Éluard, 2025
Programme formation JAT-1
Programme formation JAT-1
- Formation
- Introduction
- Poules
- Tableau à Départ en Ligne - TDL
- Tournois Multi-Chances - TMC
- Découpage
- Modules : Règles du jeu & Règlement sportif
- Exercices
- Examens
- Examen Théorique : Règles du jeu & Règlement sportif
- Examen Pratique : Tableaux
Programme formation JAT-2
Programme formation JAT-2
- Formation
- Rappel - Règlements
- Rappel - Poules
- Rappel - Tableau à Départ en Ligne - TDL
- Rappel - Tournois Multi-Chances - TMC
- Anticipation
- Tableau à Entrées Échelonnées - TEE
- Découpage
- Exercices
- Modules : Règles du jeu & Règlements sportif
- Examens
- Examen Théorique : Règles du jeu & Règlements sportif
- Examen Pratique : Tableaux
Les officiels de la compétitions
Les officiels de la compétitions
4 filières distinctes
- A - Arbitres (arbitre de chaise ou juge de ligne)
- JAE - Juges-Arbitres des rencontres par Équipes
- JAP - Juges-Arbitres de Padel
- JAT - Juges-Arbitres de Tournoi
Les officiels de la compétitions
3 niveaux
- 1 - niveau Comité
- 2 - niveau Ligue
- 3 - niveau Fédéral
Les officiels de la compétitions
Les formateurs
- FA2 et FA3
- FJAE2 et FJAE3
- FJAP2 et FJAP3
- FJAT2 et FJAT3
Compétences des JAT
Compétences des JAT1
Le JAT1 est compétent pour organiser au sein du Comité dans lequel il est licencié :
- Tennis et Paratennis :
- Tournois internes,
- Tournois NC, 5$^e$ et 4$^e$ série,
- TMC NC, 5$^e$ et 4$^e$ série (sauf exception).
- Beach tennis : BT25 et BT100 ;
- Sur dérogation, dans un autre Comité.
Le JAT1 est compétent pour être adjoint d'un JAT2 ou d'un JAT3
Compétences des JAT2
Le JAT2 est compétent pour organiser au sein de la Ligue dans laquelle il est licencié :
- toute compétition individuelle de Tennis ou Paratennis (en simple et en double) ;
- tous types de compétitions, tournoi ou championnat, de pickleball ;
- tous types de compétitions (par paires ou par équipes de club) de beach tennis (hors BT1000 et BT2000).
- Sur dérogation, dans une autre Ligue.
Le JAT2 est compétent pour être adjoint d'un JAT3
Compétences des JAT3
Le JAT3 est compétent pour organiser sur le territoire national :
Tout, selon sa ou ses spécialités de pratique
Les officiels de la compétitions
Les compétences des formateurs
Ils sont compétents pour organiser les formations, les mises à niveau techniques, les évaluations et les examens.
- niveau 2 : sur les niveaux 1 et 2 de leur qualification
- niveau 3 : sur les niveaux 1, 2 et 3 de leur qualification et les formateurs de niveau 2
Les officiels de la compétitions
Confirmation d'aptitude
Après attribution de leur qualification, les juges-arbitres sont inscrits avec le statut « actif » sur une liste d’aptitude. Cette liste est revue tous les ans, sur la base de l’activité de chacun et de l’évaluation du niveau et de la qualité de leurs prestations :
- Commission Fédérale d’Arbitrage, pour les niveaux 3 ;
- Commission Régionale d’Arbitrage, pour les niveaux 2 ;
- Commission Départementale d’Arbitrage, pour les niveaux 1 ou, en son absence, par la CRA.
Les officiels de la compétitions
Inactivité
En complément des activités minimales requises fixées en fonction du niveau de qualification par la commission fédérale d’arbitrage selon les différentes qualifications, un processus automatique inactive les qualifications selon les critères suivants :
- niveau 1 : mise en sommeil dès 5 ans d’inactivité ;
- niveau 2 : mise en sommeil dès 3 ans d’inactivité ;
- niveau 3 : mise en sommeil dès 2 ans d’inactivité.
Missions du JAT
Missions du JAT
- Présentation du Comité de Tournoi
- Préparation de la compétition :
- Vérification des inscriptions
- Établissement des poules / des tableaux
- Élaboration du planning
- Convocation des joueurs
- Gestion de la compétition :
- Contrôle des licences et des pièces d'identité
- Contrôle des certificats médicaux en cas de surclassement
- Gestion des matchs :
- Désigne l’arbitre de la partie et, éventuellement, les juges de ligne
- Gère l'attribution des terrains
- Prévoit au minimum trois balles homologuées et décide du changement des balles
- Délègue temporairement ses pouvoirs si besoin
- Statue sur les réclamations et les incidents
- Décide de l’arrêt ou de la reprise d’une partie
- Responsable de la sincérité et de l’exactitude des résultats, ainsi que de la qualité de leur transcription dans Moja.
Participation aux compétitions
Participation aux compétitions
- Sur tous les TMC (toutes pratiques) dont il a la charge, il est interdit de participer (le sien y compris) ;
- En tennis, sur un tournoi de 2$^e$ catégorie ou mieux, il est interdit de participer au tableau final de l’épreuve principale ;
- Sauf tournois internes (toute pratique),
- Sauf tournois de 3$^e$ catégorie (tennis),
- Sauf épreuves annexes des tournois de 2$^e$ catégorie et mieux (tennis),
- En Beach tennis :
- Il est interdit de participer aux BT1000 et aux BT2000 (y compris le juge-arbitre adjoint)
- Pour les BT500 et en dessous (hors TMC), le juge-arbitre devra avoir obligatoirement un adjoint lors de ses parties jouées
- Lorsqu'il participe, il doit avoir un juge-arbitre suppléant qualifié pendant la durée de sa/ses partie(s).
Le Classement
Classements de simple
- NC - non-classés
- 5$^e$ série - 40/2, 40/1 (seulement pour les jeunes)
- 4$^e$ série - 40, 30/5, 30/4, 30/3, 30/2, 30/1
- 3$^e$ série - 30, 15/5, 15/4, 15/3, 15/2, 15/1
- 2$^{de}$ série - 15, 5/6, 4/6, 3/6, 2/6, 1/6, 0, -2/6, -4/6, -15
Top 60 et Top 40 Dames, Top 100 et Top 60 Messieurs - 1$^{re}$ série - Top 20 Dames et Top 30 Messieurs
Classements de double
$$ \begin{array}{ccc} NC & : & +19 \\ \hline 40/2, 40/1, 40 & : & +18 \\ 30/5 & : & +17 \\ 30/4 & : & +16 \\ 30/3 & : & +15 \\ 30/2 & : & +14 \\ 30/1 & : & +13 \\ \hline 30 & : & +12 \\ 15/5 & : & +11 \\ 15/4 & : & +10 \\ 15/3 & : & +9 \\ 15/2 & : & +8 \\ 15/1 & : & +7 \\ \hline 15 & : & +6 \\ 5/6 & : & +5 \\ 4/6 & : & +4 \\ 3/6 & : & +3 \\ 2/6 & : & +2 \\ 1/6 & : & +1 \\ 0 & : & 0 \\ -2/6 & : & -1 \\ -4/6 & : & -2 \\ -15 & : & -3 \\ \textrm{Top 60 Dames / Top 100 Messieurs} & : & -4 \\ \textrm{Top 40 Dames / Top 60 Messieurs} & : & -5 \\ \hline 1^{re} \: \textrm{série} & : & -6 \\ \hline \textrm{Entre la 201}^e\textrm{ et la 300}^e\textrm{ place ATP ou WTA} & : & -7 \\ \textrm{Entre la 101}^e\textrm{ et la 200}^e\textrm{ place ATP ou WTA} & : & -8 \\ \textrm{Entre la 1}^{re}\textrm{ et la 100}^e\textrm{ place ATP ou WTA} & : & -9 \\ \hline \textrm{Vainqueurs Grand Chelem et vainqueurs ou finalistes Masters ATP/WTA} & : & -10 \\ \end{array} $$
Vocabulaire
Vocabulaire
- Qualifié sortant - $Q_s$
- Qualifié entrant - $q_e$
- Effectif - Nombre de joueur, $q_e$ compris
- Couple indissociable - Paire de joueurs
- Progression - Suite de deux parties avec joueur entrant
- Couloir - Succession de progressions
- Compression - 2 couloirs $\Rightarrow$ 1 couloirs
Vocabulaire sur les tableaux
- À départ en ligne (TDL) - les joueurs entrent sur un ou deux tours
- À entrées échelonnées (TEE) - les joueurs entrent sur plus de deux tours
- Classique - $Q_s = 2^p$, $Q_s = 1, 2, 4, 8, 16, \ldots$
- À sections - $Q_s \neq 2^p$, $Q_s = 3, 5, 6, 7, 9, 10, \ldots$
- Final - vainqueur de l'épreuve
Par définition, un tableau « final » est toujours un tableau « classique ».
Placement des joueurs
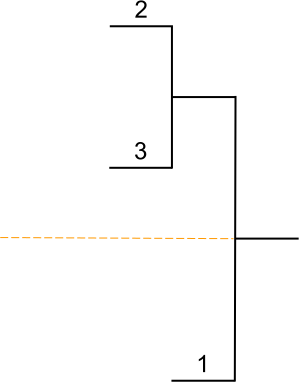
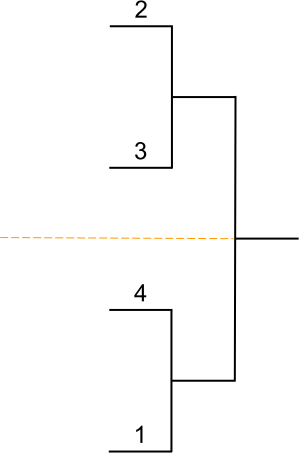
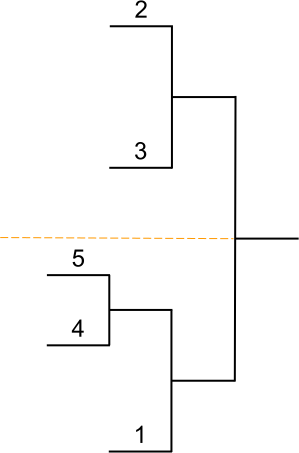
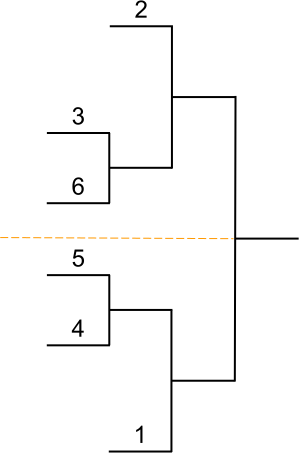
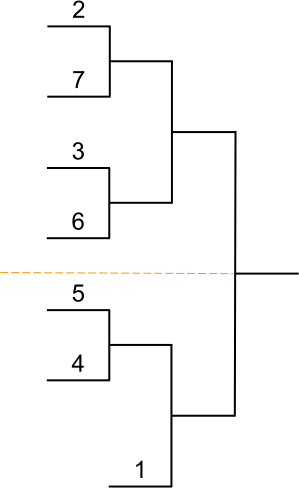
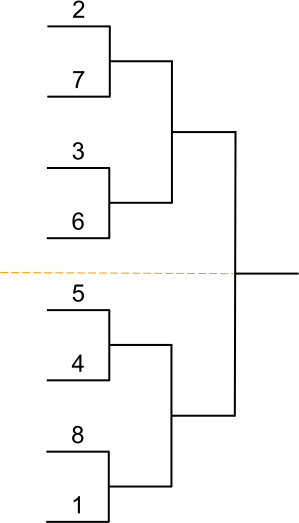
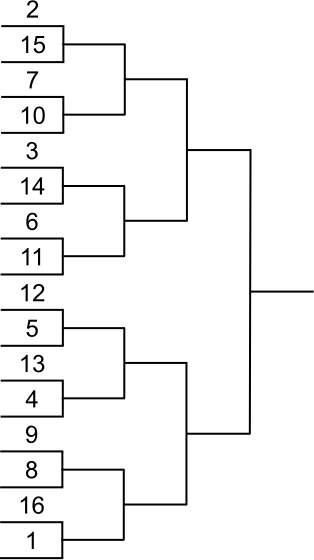
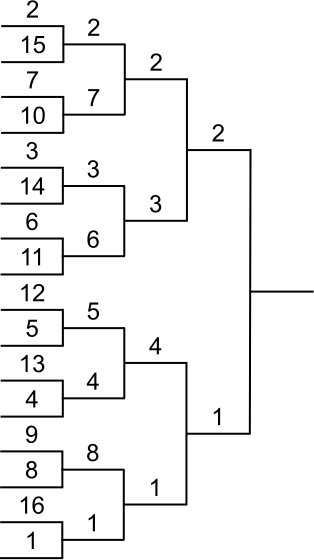
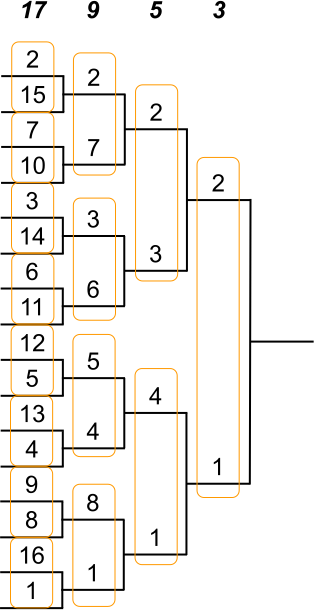
Têtes de série
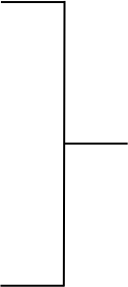
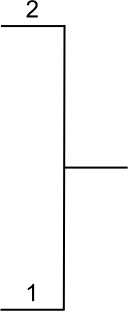
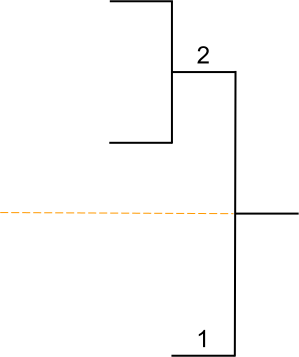
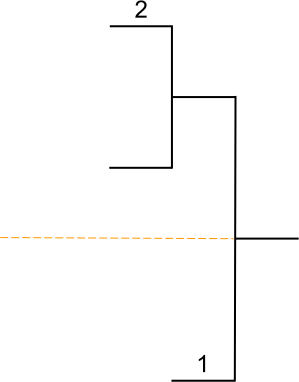
Têtes de série
Dans tout tableau comportant des joueurs classés, les joueurs les mieux classés d’entre eux doivent être placés de façon à se rencontrer le plus tard possible ; ils sont appelés têtes de série.
Tout tableau doit présenter des têtes de série, à l’exclusion de ceux qui ne comportent que des non-classés. Toutefois, un joueur non classé peut être tête de série.
Têtes de série
Le nombre de têtes de série doit être :
- Poules : 1 par poule
- Tableau intermédiaire : $Q_s$
- Tableau final : autant que la moitié des places disponibles au tour où le mieux classé est admis et au maximum de la moitié de l’effectif du tableau
- Finale $\Rightarrow$ 1 Ts
- Demi-finale $\Rightarrow$ 2 Ts
- Quart de finale $\Rightarrow$ 4 Ts
- etc.
Poules
Poules - Principe
Poules - Principe
Une épreuve avec poules est une compétition individuelle (faisant partie d’un championnat ou d’un tournoi) comprenant éventuellement 2 phases successives : une phase de poules et une phase à élimination directe.
La phase de poules peut elle-même être organisée en un enchaînement de plusieurs groupes de poules, constitués à partir des classements des joueurs, les vainqueurs des poules d’un groupe étant qualifiés pour le groupe suivant.
La phase de poules est ouverte aux joueurs Non Classés, 5$^e$ série, 4$^e$ série, 3$^e$ série et 2$^{de}$ série.
Poules - Constitution
Poules - Constitution
- Minimum 3 joueurs par poule ;
- Maximum 6 joueurs par poule ;
- Différence d'1 joueur maximum entre les poules ;
- Même classement $\Rightarrow$ Même groupe de poules ;
- Même classement $\Rightarrow$ Répartition dans les poules ;
- Meilleurs joueurs $\Rightarrow$ Têtes de série.
Conseil : 3 classements maximum en plus des qualifiés par groupe.
Poules - Têtes de série
Poules - Têtes de série
- Seulement NC $\Rightarrow$ Pas de têtes de série
- Autre que NC $\Rightarrow$ 1 tête de série par poule
- Répartition des Ts comme les joueurs
Poules - Règles de qualification
Poules - Règles de qualification
Groupe de poules $\Rightarrow$ Groupe de poules
- Même effectif = Même nombre de qualifiés sortants
- Effectif différent =
- Même nombre de qualifiés sortants
- OU 1 de plus pour les grosses poules
- Requalification du joueur suivant dans la même poule
Groupe de poules $\Rightarrow$ Groupe de poules
- Même nombre de qualifiés entrants à 1 près
- Répartition par tirage au sort
Poules - Règles de qualification
Groupe de poules $\Rightarrow$ Tableau
- Même effectif = Même nombre de qualifiés sortants
- Effectif différent =
- Même nombre de qualifiés sortants
- OU 1 de plus pour les grosses poules
- Requalification du joueur suivant dans la même poule
Groupe de poules $\Rightarrow$ Tableau
- 2 qualifiés entrants peuvent se rencontrer
- Tableau final avec seulement des qualifiés
$\Rightarrow$ TDL avec les véritables classements
Poules - Règles de qualification
Tableau $\Rightarrow$ Groupe de poules
- Même nombre de qualifiés entrants à 1 près
- Répartition par tirage au sort
Poules - Nombre de matchs
Poules - Nombre de matchs
Faire jouer des poules prend du temps
$$ \frac{n \times (n-1)}2 $$
- 3 joueurs $\Rightarrow$ 2 matchs par joueur et 3 matchs au total
- 4 joueurs $\Rightarrow$ 3 matchs par joueur et 6 matchs au total
- 5 joueurs $\Rightarrow$ 4 matchs par joueur et 10 matchs au total
- 6 joueurs $\Rightarrow$ 5 matchs par joueur et 15 matchs au total
Construction d'un groupe de poules
Construction d'un groupe de poules
Méthode du Serpentin
Exemple avec 3 poules
$ \begin{array}{c|c|c|c|c} \Rightarrow & \smile & \smile & \smile & \\ \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \\ \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ & & & & \Leftarrow \\ \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ & X & X & X & \Leftarrow \\ \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ \Downarrow & X & X & X & \Leftarrow \\ \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ \Downarrow & X & X & X & \Leftarrow \\ \Rightarrow & & & & \\ \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ \Downarrow & X & X & X & \Leftarrow \\ \Rightarrow & X & X & X & \Downarrow \\ & X & X & X & \Leftarrow \\ \hline \end{array} $ $ \begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ \Downarrow & X & X & X & \Leftarrow \\ \Rightarrow & X & X & X & \Downarrow \\ & X & X & X & \Leftarrow \\ \hline & Q_1 & Q_2 & Q_3 \\ \end{array} $ $ \begin{array}{|c|c|c|} \hline X_{\textcircled{1}} & X_{\textcircled{2}} & X_{\textcircled{3}} \\ X & X & X \\ X & X & X \\ X & X & X \\ \hline Q_1 & Q_2 & Q_3 \\ \hline \end{array} $
Exemple avec 3 poules incomplètes
\[\begin{array}{c|c|c|c|c} \Rightarrow & X & X & X & \Downarrow \\ \Downarrow & X & X & X & \Leftarrow \\ \Rightarrow & X & X & X & \Downarrow \\ & & X & X & \Leftarrow \\ \end{array}\]
Exemple avec 3 poules incomplètes
\[\begin{array}{|c|c|c|} \hline X_{\textcircled{1}} & X_{\textcircled{2}} & X_{\textcircled{3}} \\ X & X & X \\ X & X & X \\ & X & X \\ \hline Q_1 & Q_2 & Q_4 \\ & Q_3 & Q_5 \\ \hline \end{array}\]
Phases de poules
$ 9 (NC) \Rightarrow 2 \: Q_s $$ 9 (NC) \Rightarrow 2 \: Q_s $
$\begin{array}{c|c|c|c} \Rightarrow & NC & NC & \Downarrow \\ \Downarrow & NC & NC & \Leftarrow \\ \Rightarrow & NC & NC & \Downarrow \\ \Downarrow & NC & NC & \Leftarrow \\ \Rightarrow & NC & & \\ \end{array}$
$ 9 (NC) \Rightarrow 2 \: Q_s $
$\begin{array}{|c|c|} \hline NC & NC \\ NC & NC \\ NC & NC \\ NC & NC \\ NC & \\ \hline Q_1 & Q_2 \\ \hline \end{array}$
Phases de poules
$ 8 (NC) \: 4 (40) \Rightarrow 3 \: Q_s $$ 8 (NC) \: 4 (40) \Rightarrow 3 \: Q_s $
$\begin{array}{c|c|c|c|c} \Rightarrow & 40 & 40 & 40 & \Downarrow \\ \Downarrow & NC & NC & 40 & \Leftarrow \\ \Rightarrow & NC & NC & NC & \Downarrow \\ & NC & NC & NC & \Leftarrow \\ \end{array}$
$ 8 (NC) \: 4 (40) \Rightarrow 3 \: Q_s $
$\begin{array}{|c|c|c|} \hline 40_{\textcircled{1}} & 40_{\textcircled{2}} & 40_{\textcircled{3}} \\ NC & NC & 40 \\ NC & NC & NC \\ NC & NC & NC \\ \hline Q_1 & Q_2 & Q_3 \\ \hline \end{array}$
Phases de poules
$ 4 (30/4) \: 6 (30/3) \Rightarrow 4 \: Q_s $$ 4 (30/4) \: 6 (30/3) \Rightarrow 4 \: Q_s $
$\begin{array}{c|c|c|c|c} \Rightarrow & 30/3 & 30/3 & 30/3 & \Downarrow \\ \Downarrow & 30/3 & 30/3 & 30/3 & \Leftarrow \\ \Rightarrow & 30/4 & 30/4 & 30/4 & \Downarrow \\ & & & 30/4 & \Leftarrow \\ \end{array}$
$ 4 (30/4) \: 6 (30/3) \Rightarrow 4 \: Q_s $
$\begin{array}{|c|c|c|c|} \hline 30/3_{\textcircled{1}} & 30/3_{\textcircled{2}} & 30/3_{\textcircled{3}} \\ 30/3 & 30/3 & 30/3 \\ 30/4 & 30/4 & 30/4 \\ & & 30/4 \\ \hline Q_1 & Q_2 & Q_3 \\ & & Q_4 \\ \hline \end{array}$
Phases de poules
$ 5 (NC) \: 6 (40) \: 5 (30/5) \Rightarrow 4 \: Q_s $$ 5 (NC) \: 6 (40) \: 5 (30/5) \Rightarrow 4 \: Q_s $
$\begin{array}{c|c|c|c|c|c} \Rightarrow & 30/5 & 30/5 & 30/5 & 30/5 & \Downarrow \\ \Downarrow & 40 & 40 & 40 & 30/5 & \Leftarrow \\ \Rightarrow & 40 & 40 & 40 & NC & \Downarrow \\ & NC & NC & NC & NC & \Leftarrow \\ \end{array}$
$ 5 (NC) \: 6 (40) \: 5 (30/5) \Rightarrow 4 \: Q_s $
$\begin{array}{|c|c|c|c|} \hline 30/5_{\textcircled{1}} & 30/5_{\textcircled{2}} & 30/5_{\textcircled{3}} & 30/5_{\textcircled{4}} \\ 40 & 40 & 40 & 30/5 \\ 40 & 40 & 40 & NC \\ NC & NC & NC & NC \\ \hline Q_1 & Q_2 & Q_3 & Q_4 \\ \hline \end{array}$
$ 5 (NC) \: 6 (40) \: 5 (30/5) \Rightarrow 4 \: Q_s $
$\begin{array}{c|c|c|c|c} \Rightarrow & 30/5 & 30/5 & 30/5 & \Downarrow \\ \Downarrow & 40 & 30/5 & 30/5 & \Leftarrow \\ \Rightarrow & 40 & 40 & 40 & \Downarrow \\ \Downarrow & NC & 40 & 40 & \Leftarrow \\ \Rightarrow & NC & NC & NC & \Downarrow \\ & & & NC & \Leftarrow \\ \end{array}$
$ 5 (NC) \: 6 (40) \: 5 (30/5) \Rightarrow 4 \: Q_s $
$\begin{array}{|c|c|c|} \hline 30/5_{\textcircled{1}} & 30/5_{\textcircled{2}} & 30/5_{\textcircled{3}} \\ 40 & 30/5 & 30/5 \\ 40 & 40 & 40 \\ NC & 40 & 40 \\ NC & NC & NC \\ & & NC \\ \hline Q_1 & Q_2 & Q_3 \\ & & Q_4 \\ \hline \end{array}$
Phases de poules
$ 2 (q_e) \: 4 (40) \: 3 (30/5) \: 2 (30/4) \Rightarrow 2 \: Q_s $$ 2 (q_e) \: 4 (40) \: 3 (30/5) \: 2 (30/4) \Rightarrow 2 \: Q_s$
$\begin{array}{c|c|c|c} \Rightarrow & 30/4 & 30/4 & \Downarrow \\ \Downarrow &30/5 & 30/5 & \Leftarrow \\ \Rightarrow & 30/5 & 40 & \Downarrow \\ \Downarrow & 40 & 40 & \Leftarrow \\ \Rightarrow & 40 & q_e & \Downarrow \\ & q_e & \Leftarrow & \Leftarrow \\ \end{array}$
$ 2 (q_e) \: 4 (40) \: 3 (30/5) \: 2 (30/4) \Rightarrow 2 \: Q_s$
$\begin{array}{|c|c|} \hline 30/4_{\textcircled{1}} & 30/4_{\textcircled{2}} \\ 30/5 & 30/5 \\ 30/5 & 40 \\ 40 & 40 \\ 40 & q_e \\ q_e & \\ \hline Q_1 & Q_2 \\ \hline \end{array}$
Les tableaux
Les tableaux
C'est un moyen visuel qui permet à chaque joueur :
de connaître sa position dans l'épreuve
d'avoir les informations sur son adversaire
Il permet également de visualiser :
l'enchaînement des parties
les résultats
Familles de tableaux
Familles de tableaux
Tableau à Départ en Ligne ou TDL
Tableaux Multi-Chances ou TMC
Tableau à Entrées Échelonnées ou TEE
Tableau - Les 5 règles
Tableau - Les 5 règles
- Tous les joueurs de même classement doivent entrer au même tour ou sur deux tours consécutifs ; il en va de même pour les qualifiés entrant dans un tableau, quel que soit leur classement.
- Sauf dans le cas de qualifiés, il est interdit de faire entrer un joueur plus loin (c’est-à-dire aux tours suivants) qu’un joueur de classement supérieur au sien. Il en va de même pour un joueur qui n’est pas tête de série par rapport à un joueur tête de série.
- Sauf dans un tableau final à départ en ligne privilégiant le tirage au sort, il est interdit de faire rencontrer deux qualifiés issus d’un tableau précédent pour leur première partie dans le tableau.
- Tous les qualifiés sortant d'un tableau doivent être connus au même tour.
- Tous les joueurs d’un même classement doivent être admis dans le même tableau (ou groupe de poules).
Tableau - Les 8 recommandations
Tableau - Les 8 recommandations
- Adversaires des qualifiés - Les qualifiés entrants doivent, dans la mesure du possible, rencontrer les joueurs de plus faible classement directement admis dans le tableau.
- Compression - Programmer les compressions à classement égal.
- Progression des classements - Éviter qu’un joueur, après sa première partie, ne rencontre à nouveau un joueur de même classement entrant dans le tableau.
- Nombre des qualifiés
- Lorsque le nombre de qualifiés entrants le permet, éviter que deux joueurs directement admis dans un tableau ne se rencontrent dès leur première partie dans ce tableau.
- Dans le cas où les couples indissociables sont formés avec des joueurs directement admis, privilégier les couples avec des joueurs de même classement.
- Tours « en contre » programmés - Tout joueur classé devrait jouer une partie « en contre » et, sauf dans un tableau final, ne devrait jamais en jouer plus de deux.
- Écarts de classements - Respecter des écarts convenables de classements.
- Découpage en différents tableaux - Éviter d’admettre des joueurs de séries différentes dans un même tableau.
- Effectif des sections - Dans un tableau à sections, privilégier les deux
conditions suivantes :
- Toutes les sections ont le même effectif à 1 ou 2 unités près,
- Toutes les sections reçoivent le même nombre de qualifiés entrants à 1 unité près.
Tableaux à Départ en Ligne
TDL
Construction d'un TDL
NDENE
Construction d'un TDL
$Q_s \neq 2^p \Rightarrow$ Tableau à Section
$N = $ nombre de joueurs ($q_e$ oui, $Q_s$ non)
$D$ : $N \leq D=Q_s \times 2^p$
$E = D - N$
$NE = N - E$
$NPNE = NE / 2$
$Ts = Q_s$
TDL
$10(NC) \Rightarrow 4Q_s$$10(NC) \Rightarrow 4Q_s$
$Q_s = 4$
$N = 10$
$D = 16$
$E = D - N = 6$
$NE = N - E = 4$
$NPNE = NE / 2 = 2$
$Ts = 0$
TDL
$13(NC) \Rightarrow 4Q_s$$13(NC) \Rightarrow 4Q_s$
$Q_s = 4$
$N = 13$
$D = 16$
$E = D - N = 3$
$NE = N - E = 10$
$NPNE = NE / 2 = 5$
$Ts = 0$
TDL
$6(30/5) - 4(30/4) - 1(30/3) \Rightarrow 4Q_s$$6(30/5) - 4(30/4) - 1(30/3) \Rightarrow 4Q_s$
$Q_s = 4$
$N = 11$
$D = 16$
$E = D - N = 5$
$NE = N - E = 6$
$NPNE = NE / 2 = 3$
$Ts = 4$
TDL
$5(q_e) - 3(15) - 3(5/6) \Rightarrow 4Q_s$$5(q_e) - 3(15) - 3(5/6) \Rightarrow 4Q_s$
$Q_s = 4$
$N = 11$
$D = 16$
$E = D - N = 5$
$NE = N - E = 6$
$NPNE = NE / 2 = 3$
$Ts = 4$
TDL
$2(q_e) - 4(30/1) \Rightarrow 2Q_s$$2(q_e) - 4(30/1) \Rightarrow 2Q_s$
$Q_s = 2$
$N = 6$
$D = 8$
$E = D - N = 2$
$NE = N - E = 4$
$NPNE = NE / 2 = 2$
$Ts = 2$
TDL
$7(q_e) - 7(30) - 3(15/5) \Rightarrow 6Q_s$$7(q_e) - 7(30) - 3(15/5) \Rightarrow 6Q_s$
$Q_s = 6$
$N = 17$
$D = 24$
$E = D - N = 7$
$NE = N - E = 10$
$NPNE = NE / 2 = 5$
$Ts = 6$
Tableaux Multi-Chances
TMC
TMC - Principes
TMC - Principes
- Garantir un nombre de parties à tous les joueurs (2, 3, 4 ou 5)
- Classer tous les joueurs entre 1 et $n$
- Faire une succession de tableaux
- Limité à 4, 8, 16, et 32 joueurs
- Toléré à 12, et 24 joueurs
TMC - Succession de tableaux
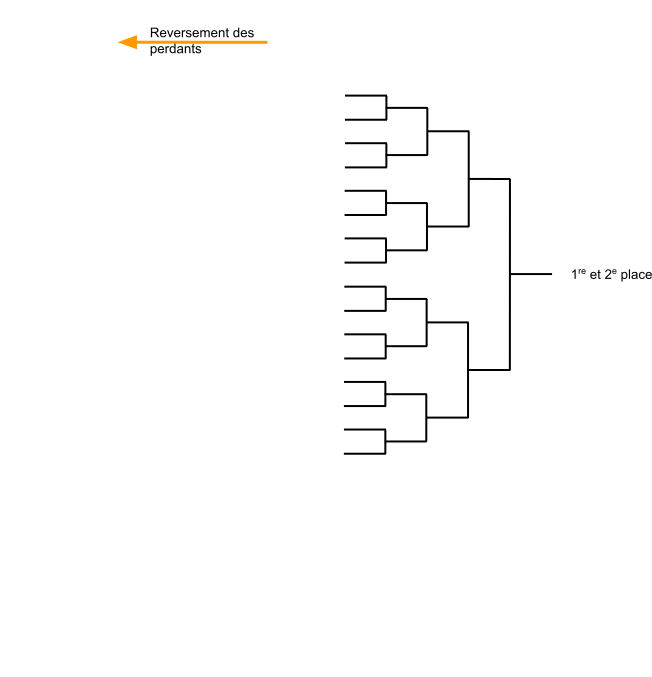
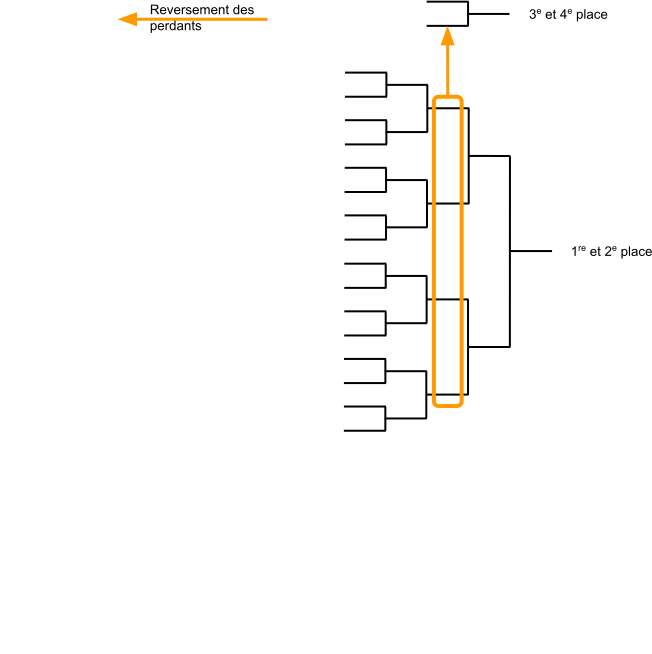
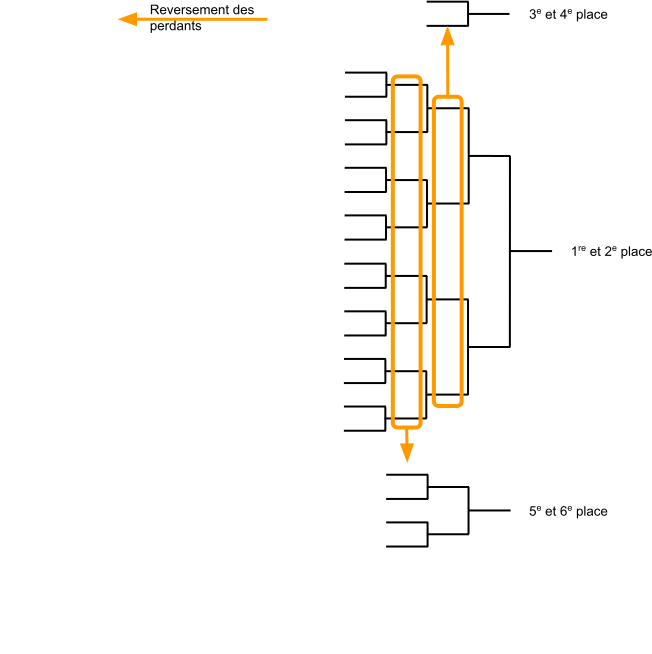
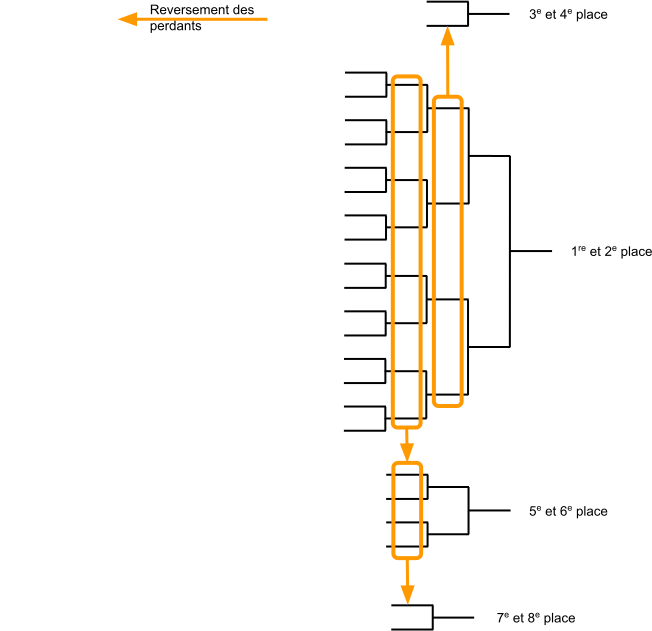
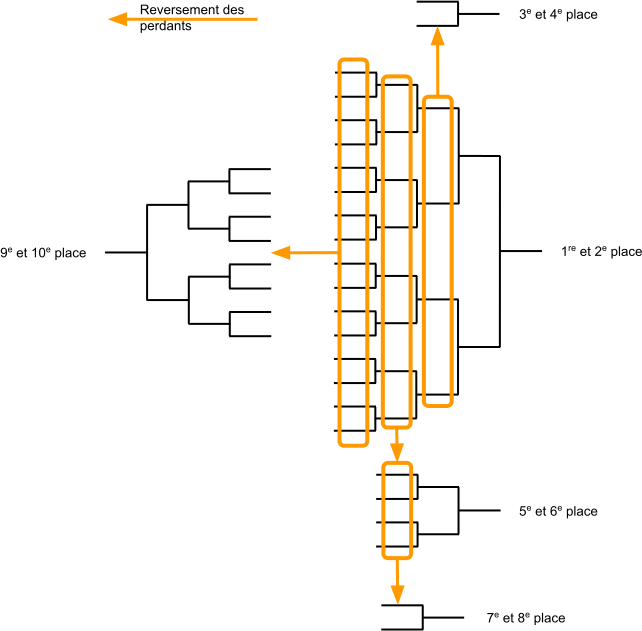
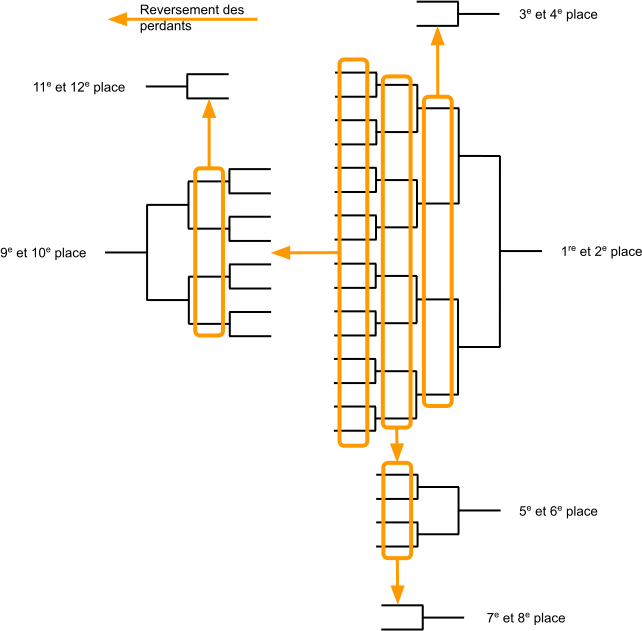
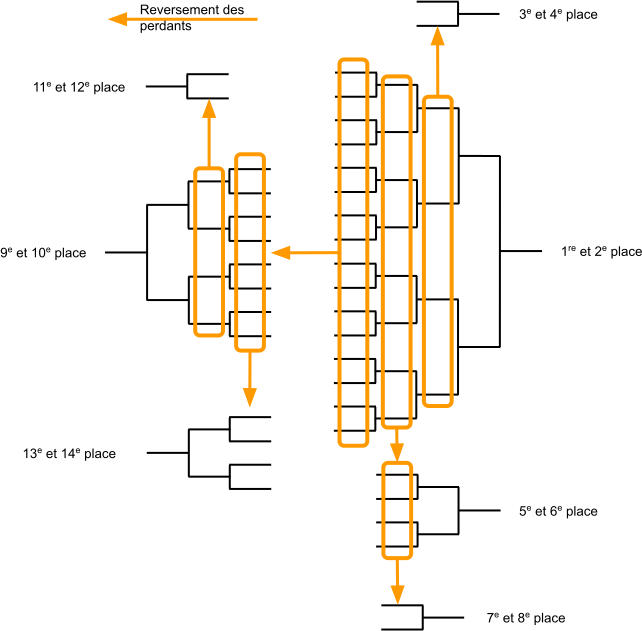
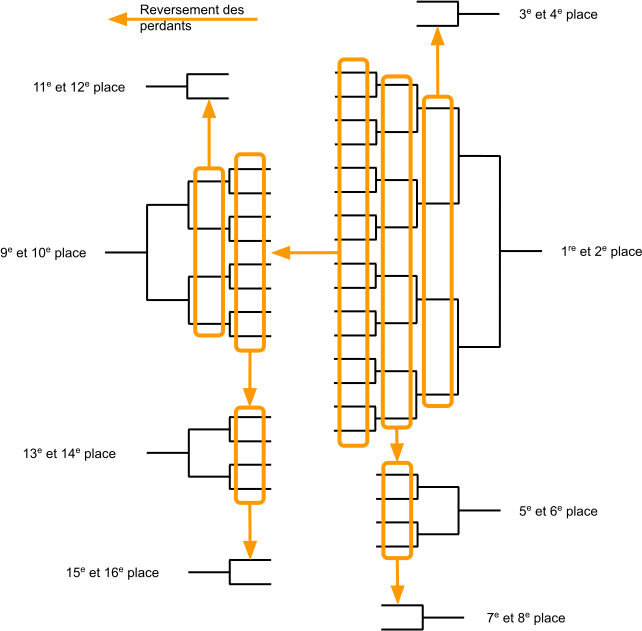
TMC - Construction
TMC - Construction
- Tableau principal $\Rightarrow$ TDL
- Tableaux de classement $\Rightarrow$ ceux qui sont prévus
- Placement des joueurs perdants $\Rightarrow$ même place que le tableau précédent
Tableaux à Entrées Échelonnées
TEE
TEE - Méthode
TEE - Méthode
Anticipation - Déterminer les couples
Escalier - Organiser l'entrée des joueurs
Tableau
Anticipation - Principe
« Ça rentre / Ça ne rentre pas »
TEE - Anticipation
- Cette méthode ne permet pas de concevoir le tableau, ce n'est pas son objectif.
- Cette méthode permet de déterminer quels sont les couples indissociables à construire afin que tout l'effectif puisse entrer dans le tableau. Elle donne donc aussi le nombre de compression.
- Le principe est de commencer par le classement le plus faible et de faire entrer les classements au fur et à mesure en s'assurant de la progression.
- Nous utilisons une colonne par classement, cela permet de vérifier rapidement s'il y a des sauts de plus d'un classement.
- Les qualifiés entrant sont particuliers, ils peuvent être sur 2 colonnes (consécutives).
- Même s'il est possible de faire ce travail sur l'intégralité des classements, nous nous arrêtons généralement dès que nous pouvons déterminer que le reste des classements pourront être intégrés sans avoir besoin de créer de nouveaux couples (il y a assez de couloirs pour le nombre de joueurs).
- Il faut toujours garder en tête qu'il faut au moins autant de couples qu'il y a de qualifiés sortants. Il ne pourra jamais y en avoir moins.
Anticipation
$5(q_e) - 5(15/3) - 5(15/2) - 3(15/1) \Rightarrow 4Q_s$
$5(q_e) - 5(15/3) - 5(15/2) - 3(15/1) \Rightarrow 4Q_s$
| 15/3 | 15/2 | 15/1 | Qs |
|---|---|---|---|
| 5 x (15/3;qe) | |||
| +5 couloirs | 5 ≤ 5 couloirs | 3 ≤ 5 couloirs | 4 ≤ 5 couloirs |
$5(q_e) - 5(15/3) - 5(15/2) - 3(15/1) \Rightarrow 4Q_s$
Effectif = 18 $Q_s$ = 4 5 couples Couples = 5x(15/3;qe) Nombre de compression = Nombre de couples - $Q_s$ = 1
Anticipation
$7(q_e) - 6(15) - 7(5/6) - 3(4/6) - 6(3/6) \Rightarrow 5Q_s$
$7(q_e) - 6(15) - 7(5/6) - 3(4/6) - 6(3/6) \Rightarrow 5Q_s$
| 15 | 5/6 | 4/6 | 3/6 | Qs |
|---|---|---|---|---|
| 6 x (15;qe) | 6 x 5/61 x (5/6;qe) | |||
| +6 couloirs | 6 ≤ 6 couloirs+1 couloir | 3 ≤ 7 couloirs | 6 ≤ 7 couloirs | 5 ≤ 7 couloirs |
$7(q_e) - 6(15) - 7(5/6) - 3(4/6) - 6(3/6) \Rightarrow 5Q_s$
Effectif = 29 $Q_s$ = 5 7 couples Couples = 6x(15;qe), 1x(5/6;qe) Nombre de compression = Nombre de couples - $Q_s$ = 2
Anticipation
$12(NC) - 2(30/5) - 4(30/4) - 2(30/3) \Rightarrow 6Q_s$
$12(NC) - 2(30/5) - 4(30/4) - 2(30/3) \Rightarrow 6Q_s$
| NC | 30/5 | 30/4 | 30/3 | Qs |
|---|---|---|---|---|
| 6 x (NC;NC) | ||||
| +6 couloirs | 2 ≤ 6 couloirs | 4 ≤ 6 couloirs | 2 ≤ 6 couloirs | 6 ≤ 6 couloirs |
$12(NC) - 2(30/5) - 4(30/4) - 2(30/3) \Rightarrow 6Q_s$
Effectif = 20 $Q_s$ = 6 6 couples Couples = 6x(NC;NC) Nombre de compression = Nombre de couples - $Q_s$ = 0
Anticipation
$3(q_e) - 5(30) - 1(15/5) - 1(15/4) \Rightarrow \textrm{Tableau final}$
$3(q_e) - 5(30) - 1(15/5) - 1(15/4) \Rightarrow \textrm{Tableau final}$
| 30 | 15/5 | 15/4 | Qs |
|---|---|---|---|
| 3 x (30;qe)1 x (30;30) | |||
| +3 couloirs+1 couloir | 1 ≤ 1 couloir | 1 ≤ 1 couloir | 1 ≤ 1 couloir |
$3(q_e) - 5(30) - 1(15/5) - 1(15/4) \Rightarrow \textrm{Tableau final}$
Effectif = 10 $Q_s$ = 1 4 couples Couples = 3x(30;qe), 1x(30;30) Nombre de compression = Nombre de couples - $Q_s$ = 3
Anticipation
$2(q_e) - 2(15/5) - 4(15/4) - 4(15/3) - 2(15/2) \Rightarrow 3Q_s$
$2(q_e) - 2(15/5) - 4(15/4) - 4(15/3) - 2(15/2) \Rightarrow 3Q_s$
| 15/5 | 15/4 | 15/3 | 15/2 | Qs |
|---|---|---|---|---|
| 2 x (15/5;qe) | 2 x 15/41 x (15/4;15/4) | 2 x 15/31 x (15/3;15/3) | ||
| +2 couloirs | 2 ≤ 2 couloirs+1 couloir | 2 ≤ 3 couloirs+1 couloir | 2 ≤ 4 couloirs | 3 ≤ 4 couloirs |
$2(q_e) - 2(15/5) - 4(15/4) - 4(15/3) - 2(15/2) \Rightarrow 3Q_s$
Effectif = 14 $Q_s$ = 3 4 couples Couples = 2x(15/5;qe), 1x(15/4;15/4), 1x(15/3;15/3) Nombre de compression = Nombre de couples - $Q_s$ = 1
Anticipation
$4(30) - 2(15/5) - 6(15/4) - 3(15/3) - 3(15/2) - 3(15/1) \Rightarrow 4Q_s$
$4(30) - 2(15/5) - 6(15/4) - 3(15/3) - 3(15/2) - 3(15/1) \Rightarrow 4Q_s$
| 30 | 15/5 | 15/4 | 15/3 | 15/2 | 15/1 | Qs |
|---|---|---|---|---|---|---|
| 2 x (30;30) | 2 x 15/5 | 2 x 15/42 x (15/4;15/4) | ||||
| +2 couloirs | 2 ≤ 2 couloirs | 2 ≤ 2 couloirs+2 couloirs | 3 ≤ 4 couloirs | 3 ≤ 4 couloirs | 3 ≤ 4 couloirs | 4 ≤ 4 couloirs |
$4(30) - 2(15/5) - 6(15/4) - 3(15/3) - 3(15/2) - 3(15/1) \Rightarrow 4Q_s$
Effectif = 21 $Q_s$ = 4 4 couples Couples = 2x(30;30), 2x(15/4;15/4) Nombre de compression = Nombre de couples - $Q_s$ = 0
Anticipation
$4(q_e) - 4(15) - 3(5/6) - 2(4/6) - 1(3/6) - 2(2/6) \Rightarrow \textrm{Tableau final}$
$4(q_e) - 4(15) - 3(5/6) - 2(4/6) - 1(3/6) - 2(2/6) \Rightarrow \textrm{Tableau final}$
| 15 | 5/6 | 4/6 | 3/6 | 2/6 | Qs |
|---|---|---|---|---|---|
| 4 x (15;qe) | |||||
| +4 couloirs | 3 ≤ 4 couloirs | 2 ≤ 4 couloirs | 1 ≤ 4 couloir | 2 ≤ 4 couloirs | 1 ≤ 4 couloir |
$4(q_e) - 4(15) - 3(5/6) - 2(4/6) - 1(3/6) - 2(2/6) \Rightarrow \textrm{Tableau final}$
Effectif = 16 $Q_s$ = 1 4 couples Couples = 4x(15;qe) Nombre de compression = Nombre de couples - $Q_s$ = 3Le meilleur classement entre en 1/2 finaleTs = 2
Méthode fédérale
« Escalier »
Escalier - Principe
Escalier - Principe
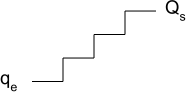
Escalier - Observations
Escalier - Observations
- Effectif total : Nombre de joueurs à positionner dans le tableaux
- Nombre de qualifiés sortants ($Q_s$): Capacité d'accueil de la phase suivante
- Couples indissociables : Paires de joueurs utilisées pour commencer un couloir (utiliser les résultats de l'anticipation)
- Nombre de compressions : Création d'un couloir unique issu de la fusion de deux couloirs existants (utiliser les résultats de l'anticipation)
- Nombre de têtes de série : Les meilleurs joueurs du tableau
Escalier - Méthode
Escalier - Méthode
- Construction de la dernière marche : Créer la marche finale avec le nombre de qualifiés sortants ($Q_s$). C’est le nombre de places disponibles pour cette marche ($N_q = Q_s$)
- Construction des marches précédentes :
- Calcul du nombre de places disponibles sur cette marche ($N$) : Doubler le nombre de places disponibles sur la marche suivante ($N = 2 \times N_q$)
- Détermination des admis à cette marche ($N_a$) : au choix du juge-arbitre en fonction des classements disponibles
- Détermination du nombre de places restantes ($N_q$) : Soustraire le nombre d’admis au nombre de places de la marche ($N_q = N - N_a$)
- Calcul du nombre de compressions ($\bullet$): Évaluer le nombre de couloirs inutilisés
- Répétition du processus : Répéter ces calculs pour chaque marche en descendant l’escalier, en utilisant à chaque fois le nombre de places disponibles de la marche suivante ($N_q$)
Escalier
$5(q_e) - 5(15/3) - 5(15/2) - 3(15/1) \Rightarrow 4Q_s$
$5(q_e) - 5(15/3) - 5(15/2) - 3(15/1) \Rightarrow 4Q_s$
| 15/3 |
|---|
| 5 x (15/3;qe) |
$5(q_e) - 5(15/3) - 5(15/2) - 3(15/1) \Rightarrow 4Q_s$
Effectif = 18 $Q_s$ = 4 5 couples Couples = 5x(15/3;qe) Nombre de compression = Nombre de couples - $Q_s$ = 1 Ts = 4
$5(q_e) - 5(15/3) - 5(15/2) - 3(15/1) \Rightarrow 4Q_s$
| 105x(15/3;qe)0 | $\rightarrow$ | 105x15/25 | $\rightarrow$ | 83x15/15 | $\rightarrow$ | 4 |
| • = 0 | • = 0 | • = 1 |
Escalier
$7(q_e) - 6(15) - 7(5/6) - 3(4/6) - 6(3/6) \Rightarrow 5Q_s$
$7(q_e) - 6(15) - 7(5/6) - 3(4/6) - 6(3/6) \Rightarrow 5Q_s$
| 15 | 5/6 |
|---|---|
| 6 x (15;qe) | 6 x 5/61 x (5/6;qe) |
| +6 couloirs | 6 ≤ 6 couloirs+1 couloir |
$7(q_e) - 6(15) - 7(5/6) - 3(4/6) - 6(3/6) \Rightarrow 5Q_s$
Effectif = 29 $Q_s$ = 5 7 couples Couples = 6x(15;qe), 1x(5/6;qe) Nombre de compression = Nombre de couples - $Q_s$ = 2 Ts = 5
$7(q_e) - 6(15) - 7(5/6) - 3(4/6) - 6(3/6) \Rightarrow 5Q_s$
| 126x(15;qe)0 | $\rightarrow$ | 146x5/61x(5/6;qe)6 | $\rightarrow$ | 122x3/63x4/67 | $\rightarrow$ | 104x3/66 | $\rightarrow$ | 5 |
| • = 0 | • = 0 | • = 1 | • = 1 |
Escalier
$12(NC) - 2(30/5) - 4(30/4) - 2(30/3) \Rightarrow 6Q_s$
$12(NC) - 2(30/5) - 4(30/4) - 2(30/3) \Rightarrow 6Q_s$
| NC |
|---|
| 6 x (NC;NC) |
| +6 couloirs |
$12(NC) - 2(30/5) - 4(30/4) - 2(30/3) \Rightarrow 6Q_s$
Effectif = 20 $Q_s$ = 6 6 couples Couples = 6x(NC;NC) Nombre de compression = Nombre de couples - $Q_s$ = 0 Ts = 6
$12(NC) - 2(30/5) - 4(30/4) - 2(30/3) \Rightarrow 6Q_s$
| 42x(NC;NC)0 | $\rightarrow$ | 122x30/54x(NC;NC)2 | $\rightarrow$ | 122x30/34x30/46 | $\rightarrow$ | 6 |
| • = 0 | • = 0 | • = 0 |
Escalier
$3(q_e) - 5(30) - 1(15/5) - 1(15/4) \Rightarrow \textrm{Tableau final}$
$3(q_e) - 5(30) - 1(15/5) - 1(15/4) \Rightarrow \textrm{Tableau final}$
| 30 |
|---|
| 3 x (30;qe)1 x (30;30) |
| +3 couloirs+1 couloir |
$3(q_e) - 5(30) - 1(15/5) - 1(15/4) \Rightarrow \textrm{Tableau final}$
Effectif = 10 $Q_s$ = 1 4 couples Couples = 3x(30;qe), 1x(30;30) Nombre de compression = Nombre de couples - $Q_s$ = 3 Le meilleur classement entre en 1/2 finale Ts = 2
$3(q_e) - 5(30) - 1(15/5) - 1(15/4) \Rightarrow \textrm{Tableau final}$
| 81x(30;30)3x(30;qe)0 | $\rightarrow$ | 44 | $\rightarrow$ | 41x15/51x15/42 | $\rightarrow$ | 22 | $\rightarrow$ | 1 |
| • = 0 | • = 2 | • = 0 | • = 1 |
Escalier
$2(q_e) - 2(15/5) - 4(15/4) - 4(15/3) - 2(15/2) \Rightarrow 3Q_s$
$2(q_e) - 2(15/5) - 4(15/4) - 4(15/3) - 2(15/2) \Rightarrow 3Q_s$
| 15/5 | 15/4 | 15/3 |
|---|---|---|
| 2 x (15/5;qe) | 2 x 15/41 x (15/4;15/4) | 2 x 15/31 x (15/3;15/3) |
| +2 couloirs | 2 ≤ 2 couloirs+1 couloir | 2 ≤ 3 couloirs+1 couloir |
$2(q_e) - 2(15/5) - 4(15/4) - 4(15/3) - 2(15/2) \Rightarrow 3Q_s$
Effectif = 14 $Q_s$ = 3 4 couples Couples = 2x(15/5;qe), 1x(15/4;15/4), 1x(15/3;15/3) Nombre de compression = Nombre de couples - $Q_s$ = 1 Ts = 3
$2(q_e) - 2(15/5) - 4(15/4) - 4(15/3) - 2(15/2) \Rightarrow 3Q_s$
| 21x(15/5;qe)0 | $\rightarrow$ | 61x15/41x(15/5;qe)1x(15/4;15/4)1 | $\rightarrow$ | 81x15/42x15/31x(15/3;15/3)3 | $\rightarrow$ | 62x15/24 | $\rightarrow$ | 3 |
| • = 0 | • = 0 | • = 0 | • = 1 |
Escalier
$4(30) - 2(15/5) - 6(15/4) - 3(15/3) - 3(15/2) - 3(15/1) \Rightarrow 4Q_s$
$4(30) - 2(15/5) - 6(15/4) - 3(15/3) - 3(15/2) - 3(15/1) \Rightarrow 4Q_s$
| 30 | 15/5 | 15/4 |
|---|---|---|
| 2 x (30;30) | 2 x 15/5 | 2 x 15/42 x (15/4;15/4) |
| +2 couloirs | 2 ≤ 2 couloirs | 2 ≤ 2 couloirs+2 couloirs |
$4(30) - 2(15/5) - 6(15/4) - 3(15/3) - 3(15/2) - 3(15/1) \Rightarrow 4Q_s$
Effectif = 21 $Q_s$ = 4 4 couples Couples = 2x(30;30), 2x(15/4;15/4) Nombre de compression = Nombre de couples - $Q_s$ = 0 Ts = 4
$4(30) - 2(15/5) - 6(15/4) - 3(15/3) - 3(15/2) - 3(15/1) \Rightarrow 4Q_s$
| 21x(30;30)0 | $\rightarrow$ | 41x15/51x(30;30)1 | $\rightarrow$ | 41x15/41x15/52 | $\rightarrow$ | 81x15/41x15/32x(15/4;15/4)2 | $\rightarrow$ | 82x15/22x15/34 | $\rightarrow$ | 83x15/11x15/24 | $\rightarrow$ | 4 |
| • = 0 | • = 0 | • = 0 | • = 0 | • = 0 | • = 0 |
Escalier
$4(q_e) - 4(15) - 3(5/6) - 2(4/6) - 1(3/6) - 2(2/6) \Rightarrow \textrm{Tableau final}$
$4(q_e) - 4(15) - 3(5/6) - 2(4/6) - 1(3/6) - 2(2/6) \Rightarrow \textrm{Tableau final}$
| 15 |
|---|
| 4 x (15;qe) |
| +4 couloirs |
$4(q_e) - 4(15) - 3(5/6) - 2(4/6) - 1(3/6) - 2(2/6) \Rightarrow \textrm{Tableau final}$
Effectif = 16 $Q_s$ = 1 4 couples Couples = 4x(15;qe) Nombre de compression = Nombre de couples - $Q_s$ = 3 Le meilleur classement entre en 1/2 finale Ts = 2
$4(q_e) - 4(15) - 3(5/6) - 2(4/6) - 1(3/6) - 2(2/6) \Rightarrow \textrm{Tableau final}$
| 84x(15;qe)0 | $\rightarrow$ | 62x5/64 | $\rightarrow$ | 61x5/62x4/63 | $\rightarrow$ | 41x3/63 | $\rightarrow$ | 42x2/62 | $\rightarrow$ | 22 | $\rightarrow$ | 1 |
| • = 0 | • = 1 | • = 0 | • = 1 | • = 0 | • = 1 |
Découpages
Découpage - Méthode
Découpage
Rappel sur les recommandations
Recommandation n°1
Les qualifiés entrants doivent, dans la mesure du possible, rencontrer les joueurs de plus faible classement directement admis dans le tableau.
Recommandation n°4.1
Lorsque le nombre de qualifiés entrants le permet, éviter que deux joueurs directement admis dans un tableau ne se rencontrent dès leur première partie dans ce tableau.
Recommandation n°4.2
Dans le cas où les couples indissociables sont formés avec des joueurs directement admis, privilégier les couples avec des joueurs de même classement.
Recommandation n°6
Respecter des écarts convenables de classements.
Recommandation n°7
Éviter d’admettre des joueurs de séries différentes dans un même tableau.
Progression sans saut de classement.
Maximisation des sortants, souvent un sureffectif sur le classement entrant.
Maximisation des entrants, souvent un sureffectif sur le classement sortant.
$$ Q = 1, 2, 3, 4 \ldots , min (effectif) $$
Il faut maintenant déterminer les valeurs à écarter.
Découpage
$ 4(q_e) \: 3(30/5) \: 4(30/4) \: \mid \: 4(30/3) \: \mid \: 2(30/2) \: 2(30/1) \Rightarrow 4 \: Q_s $
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & \times \\ 1: & \smile & 4 & \blacksquare & 4 & \smile \\ 2: & 3 & 4 & \blacksquare & 4 & \smile \\ 3: & \smile & 4 & \blacksquare & 4 & \times \\ \end{array} $$
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & \times \\ 1: & \smile & 4 & \blacksquare & 4 & \smile & 1,2,3,4 \\ 2: & 3 & 4 & \blacksquare & 4 & \smile & 1,2,3,4 \\ 3: & \smile & 4 & \blacksquare & 4 & \times & 1,2,3,4 \\ \end{array} $$
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & \times \\ 1: & \smile & 4 & \blacksquare & 4 & \smile & \cancel{1},2,\cancel{3},4 \\ 2: & 3 & 4 & \blacksquare & 4 & \smile & \cancel{1},2,\cancel{3},4 \\ 3: & \smile & 4 & \blacksquare & 4 & \times & \cancel{1},2,\cancel{3},4 \\ \end{array} $$
Entre 30/3 et 30/2
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & \times & 30/3 & \blacksquare & 30/2 & 30/1 \\ 1: & \smile & 4 & \blacksquare & 2 & \smile \\ 2: & \times & 4 & \blacksquare & 2 & \smile \\ 3: & \smile & 4 & \blacksquare & 2 & 2 \\ \end{array} $$
Entre 30/3 et 30/2
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & \times & 30/3 & \blacksquare & 30/2 & 30/1 \\ 1: & \smile & 4 & \blacksquare & 2 & \smile & 1,2 \\ 2: & \times & 4 & \blacksquare & 2 & \smile & 1,2 \\ 3: & \smile & 4 & \blacksquare & 2 & 2 & 1,2,3,4 \\ \end{array} $$
Entre 30/3 et 30/2
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & \times & 30/3 & \blacksquare & 30/2 & 30/1 \\ 1: & \smile & 4 & \blacksquare & 2 & \smile & \cancel{1},2 \\ 2: & \times & 4 & \blacksquare & 2 & \smile & \cancel{1},2 \\ 3: & \smile & 4 & \blacksquare & 2 & 2 & \cancel{1},2,3,4 \\ \end{array} $$
Découpage
$ 8(q_e) \: 7(30/5) \: 6(30/4) \: \mid \: 5(30/3) \: 3(30/2) \: \mid \: 8 (30/1) \Rightarrow 6(30) \: 2 (15/5) $
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & 30/2 \\ 1: & \smile & 6 & \blacksquare & 5 & \smile \\ 2: & 7 & 6 & \blacksquare & 5 & \smile \\ 3: & \smile & 6 & \blacksquare & 5 & 3 \\ \end{array} $$
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & 30/2 \\ 1: & \smile & 6 & \blacksquare & 5 & \smile & 1,2,3,4,5 \\ 2: & 7 & 6 & \blacksquare & 5 & \smile & 1,2,3,4,5 \\ 3: & \smile & 6 & \blacksquare & 5 & 3 & 1,2,3,4,5,6 \\ \end{array} $$
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & 30/2 \\ 1: & \smile & 6 & \blacksquare & 5 & \smile & 1,\cancel{2},3,\cancel{4},5 \\ 2: & 7 & 6 & \blacksquare & 5 & \smile & 1,\cancel{2},3,\cancel{4},5 \\ 3: & \smile & 6 & \blacksquare & 5 & 3 & 1,\cancel{2},3,\cancel{4},5,6 \\ \end{array} $$
Entre 30/2 et 30/1
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/3 & 30/2 & \blacksquare & 30/1 & \times \\ 1: & \smile & 3 & \blacksquare & 8 & \smile \\ 2: & 5 & 3 & \blacksquare & 8 & \smile \\ 3: & \smile & 3 & \blacksquare & 8 & \times \\ \end{array} $$
Entre 30/2 et 30/1
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/3 & 30/2 & \blacksquare & 30/1 & \times \\ 1: & \smile & 3 & \blacksquare & 8 & \smile & 1,2,3 \\ 2: & 5 & 3 & \blacksquare & 8 & \smile & 1,2,3,4,5,6,7,8 \\ 3: & \smile & 3 & \blacksquare & 8 & \times & 1,2,3 \\ \end{array} $$
Entre 30/2 et 30/1
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/3 & 30/2 & \blacksquare & 30/1 & \times \\ 1: & \smile & 3 & \blacksquare & 8 & \smile & \cancel{1},2,\cancel{3} \\ 2: & 5 & 3 & \blacksquare & 8 & \smile & \cancel{1},2,\cancel{3},4,\cancel{5},6,\cancel{7},8 \\ 3: & \smile & 3 & \blacksquare & 8 & \times & \cancel{1},2,\cancel{3} \\ \end{array} $$
Entre 30/1 et 30
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & \times & 30/1 & \blacksquare & 30 & 15/5 \\ 1: & \smile & 8 & \blacksquare & 6 & \smile \\ 2: & \times & 8 & \blacksquare & 6 & \smile \\ 3: & \smile & 8 & \blacksquare & 6 & 2 \\ \end{array} $$
Entre 30/1 et 30
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & \times & 30/1 & \blacksquare & 30 & 15/5 \\ 1: & \smile & 8 & \blacksquare & 6 & \smile & 1,2,3,4,5,6 \\ 2: & \times & 8 & \blacksquare & 6 & \smile & 1,2,3,4,5,6 \\ 3: & \smile & 8 & \blacksquare & 6 & 2 & 1,2,3,4,5,6,7,8 \\ \end{array} $$
Entre 30/1 et 30
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & \times & 30/1 & \blacksquare & 30 & 15/5 \\ 1: & \smile & 8 & \blacksquare & 6 & \smile & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ 2: & \times & 8 & \blacksquare & 6 & \smile & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ 3: & \smile & 8 & \blacksquare & 6 & 2 & \cancel{1},2,\cancel{3},4,\cancel{5},6,7,8 \\ \end{array} $$
Découpage
$ 8(40) \: 8(30/5) \: 6(30/4) \: \mid \: 6(30/3) \: 5(30/2) \: 6(30/1) \Rightarrow 6 (30) $
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & 30/2 \\ 1: & \smile & 6 & \blacksquare & 6 & \smile \\ 2: & 8 & 6 & \blacksquare & 6 & \smile \\ 3: & \smile & 6 & \blacksquare & 6 & 5 \\ \end{array} $$
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & 30/2 \\ 1: & \smile & 6 & \blacksquare & 6 & \smile & 1,2,3,4,5,6 \\ 2: & 8 & 6 & \blacksquare & 6 & \smile & 1,2,3,4,5,6 \\ 3: & \smile & 6 & \blacksquare & 6 & 5 & 1,2,3,4,5,6 \\ \end{array} $$
Entre 30/4 et 30/3
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/5 & 30/4 & \blacksquare & 30/3 & 30/2 \\ 1: & \smile & 6 & \blacksquare & 6 & \smile & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ 2: & 8 & 6 & \blacksquare & 6 & \smile & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ 3: & \smile & 6 & \blacksquare & 6 & 5 & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ \end{array} $$
Entre 30/1 et 30
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/2 & 30/1 & \blacksquare & 30 & \times \\ 1: & \smile & 6 & \blacksquare & 6 & \smile \\ 2: & 5 & 6 & \blacksquare & 6 & \smile \\ 3: & \smile & 6 & \blacksquare & 6 & \times \\ \end{array} $$
Entre 30/1 et 30
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/2 & 30/1 & \blacksquare & 30 & \times \\ 1: & \smile & 6 & \blacksquare & 6 & \smile & 1,2,3,4,5,6 \\ 2: & 5 & 6 & \blacksquare & 6 & \smile & 1,2,3,4,5,6 \\ 3: & \smile & 6 & \blacksquare & 6 & \times & 1,2,3,4,5,6 \\ \end{array} $$
Entre 30/1 et 30
$$ \begin{array}{ccccccc} & & & Q & & \\ & & Q_s && q_e & \\ & & \longleftarrow && \longrightarrow & \\ & 30/2 & 30/1 & \blacksquare & 30 & \times \\ 1: & \smile & 6 & \blacksquare & 6 & \smile & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ 2: & 5 & 6 & \blacksquare & 6 & \smile & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ 3: & \smile & 6 & \blacksquare & 6 & \times & \cancel{1},2,\cancel{3},4,\cancel{5},6 \\ \end{array} $$